Octave
Example in WebMiau
Octave
Overview
Octave problems are problems where the user has to write Octave code as the answer. The answer may
consist of one or more fragments of Octave code and one or more Octave functions. Both of them are
input in text fields on the problem's HTML page.
The correction is done by Octave as well. The author writes an Octave script, the so-called evaluator.
Optionally, the author can write one or more Octave functions. We call them author functions to distinguish
them from the functions defined by the user as part of the answer. The latter we call user functions. The purpose of
the evaluator is to check and grade the answer. To this end, the evaluator is executed in an Octave process when
the problem is corrected. From within the evaluator and the author functions, the author has access to the user code
fragments by placeholders of the form
@@USER_ANSWER_1@@, @@USER_ANSWER_2@@, ...
where @@USER_ANSWER_<n>@@ stands for the <n>-th code fragment. @@USER_ANSWER@@ is equivalent to @@USER_ANSWER_1@@.
The placeholders are substituted by the respective code fragments before the evaluator is executed. The user functions
can simply be called by name in the evaluator and the author functions.
The result of the correction is expressed by the exit value of the Octave process running the evaluator. 0 means
the user's answer is completely correct and the score is 1. Exit values other than 0 express answers that are entirely or partly
wrong. For each exit value (except 0), the author can specify a score value and a feedback in the TeX source. The
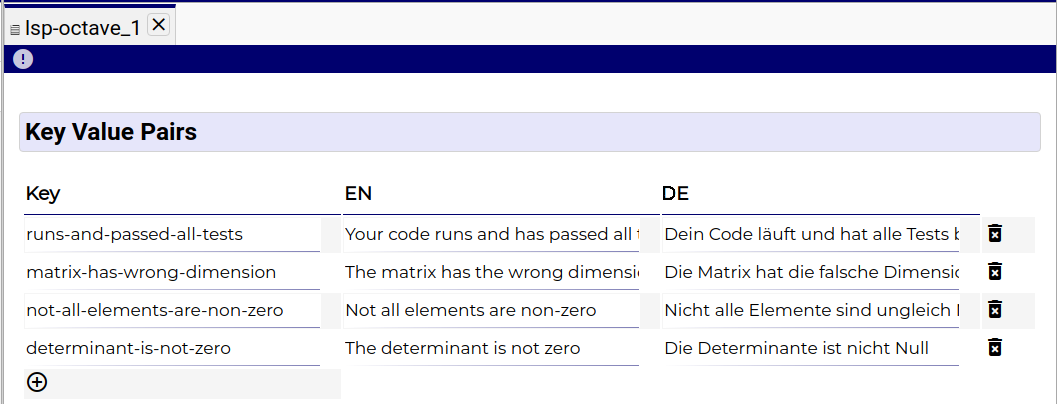
feedback is specified by an LSP key.
TeX commands/environments
The TeX commands and environments which are specific to Octave problems are listed below:
\octanswer
\octanswer[<count>]{<rows>}{<cols>}
|
Creates an input field for a code fragment.
<rows> Number of rows of the input field<cols> Number of columns of the input field<count> Number of the code fragment. If omitted, the largest number used so far in an \octanswer command or
octanswer environment increased by 1 is used.
Example:
octsolution
\begin{octsolution}[<count>]
...
\end{octsolution}
|
Creates a sample solution for the <count>-th code fragment. If <count> is omitted, the largest number used so far in an
octsolution environment increased by 1 is used.
Example:
\begin{octsolution}
[0, 2, 3]
\end{octsosultion}
|
\octfunctionanswer
\octfunctionanswer{<name>}{<rows>}{<cols>}
|
Creates an input field for a function that has to be defined by the user as part of the answer.
<name> Name of the function<rows> Number of rows of the input field<cols> Number of columns of the input field
Example:
\octfunctionanswer{compute_min}{20}{80}
|
octfunctionsolution
\begin{octfunctionsolution}{<name>}
...
\end{octfunctionsolution}
|
Creates a sample solution for a function that has to be defined by the user as part of the answer.
<name> Name of the function
Example:
\begin{octfunctionsolution}{compute_min}
function min = mymin (A)
min = false;
for i = 1:rows(A)
for j = 1:columns(A)
a = A(i,j);
if ( or(min == false, a > min) )
min = a;
endif
endfor
endfor
endfunction
\end{octfunctionsolution}
|
octevaluator
\begin{octevaluator}
...
\end{octevaluator}
|
Defines the evaluator code.
octfunction
\begin{octfunction}{<name>}
...
\end{octfunction}
|
Creates an author function. <name> is the name of the function.
\octgrading
\octgrading{<exit_value>}{<score>}{<feedback_lsp_key>}
|
Specifies the grade and the feedback for a certain exit value.
<exit_value> Exit value of the Octave process running the evaluator<score> Score value<feedback_lsp_key> LSP key of the feedback.
Please note: There is no full support for Octave problems in WebMiau yet. Thus, it is recommended that you
publish your Octave problems on a MUMIE server to test them.
Let us create a simple Octave problem. The user has to define a matrix in Octave that has dimension 3x3, determinant 0,
and only non-zero elements. Start with opening WebMiau and navigating in the checkin tree to the section where you want
to create the problem.
Right-click on the section, choose "New Document", select type "Problem", select the template Octave and choose a name
for the document. In this example, we use "octave_1". Click "Save".
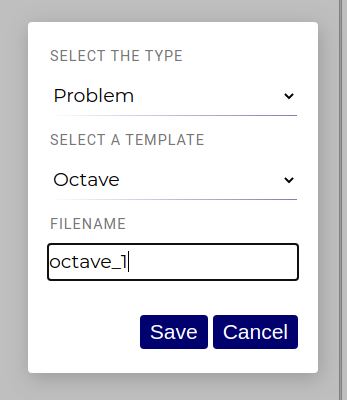
You should see the following template in the editor:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 | Describe problem here...
\octanswer{12}{80} % <-- Change this
\octfunctionanswer{matrix_min}{12}{80} % <-- Change this
\begin{hidden}
\begin{octsolution} % <-- Change this
% <-- Fill in code here
\end{octsolution}
\begin{octfunctionsolution}{matrix_min} % <-- Change this
% <-- Fill in code here
\end{octfunctionsolution}
\begin{octfunction}{expected_matrix_min} % <-- Change this
% <-- Fill in code here
\end{octfunction}
\begin{octevaluator}
% <-- Fill in code here
\end{octevaluator}
\octgrading{0}{1.0}{runs-and-passed-all-tests} %
\octgrading{1}{0.0}{code-caused-runtime-error} % <-- Change this
\octgrading{11}{0.5}{wrong-for-empty-matrices} %
\end{hidden}
|
Delete the \octfunctionanswer, octfunctionsolution, and octfunction commands resp. environments; they are not
needed in our example. Change the rest of the code as follows:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 | \title{Determinant}
Write a $3\times3$ matrix that has determinant $0$ and none of its elements zero.
\octanswer{6}{80}
\begin{hidden}
\begin{octsolution}
[ 1, 2, 3; -2, 1, 1; 2, -1, -1]
\end{octsolution}
\begin{octevaluator}
A = @USER_ANSWER@;
if ( or(rows(A) != 3, columns(A) != 3) )
exit(10);
endif
for i = 1:rows(A)
for j = 1:columns(A)
if ( A(i,j) == 0 )
exit(11);
endif
endfor
endfor
if ( det(A) != 0 )
exit(12)
endif
exit(0);
\end{octevaluator}
\octgrading{0}{1.0}{runs-and-passed-all-tests}
\octgrading{1}{0.0}{code-caused-runtime-error}
\octgrading{10}{0.0}{matrix-has-wrong-dimension}
\octgrading{11}{0.0}{not-all-elements-are-non-zero}
\octgrading{12}{0.0}{determinant-is-not-zero}
\end{hidden}
|
Let's go through the parts of the document:
The \octanswer command defines a text field where the user can input the anser, which is a code fragment in this case.
The input field has 6 rows and 80 columns.
The octsolution environment defines a sample solution. It is displayed in the correction.
The octevaluator environmet defines the evaluator. Note how the user answer is imported with the @@USER_ANSWER@@
placeholder. The evaluator first checks if the matrix
has the correct dimension ($$3\times3$$). If it has not, the Octave process is terminated with exit code 10 by means of
the exit command. The evaluator then checks if all matrix elements are non-zero. If it finds a matrix element that is
zero, it terminates the execution with exit code 11. Finally, the evaluator checks if the determinant is 0.
If this is not the case, the execution is terminated with exit code 12. Otherwise, the execution is terminated with exit
code 0.
The \octgrading commands specify which grade values and feedbacks correspond to the exit codes above. For example,
the exit code 11 results in grade 0.0 (i.e., 0 points) and the
feedback "not-all-elements-are-non-zero". The latter is the name of a LSP variable. The actual feedback that shows up
in the correction is the value of the LSP variable in the
current language.
The LSP variables not defined yet; we have to do that in an LSP sheet and reference the LSP sheet in the problem.
Let's create a new LSP sheet for that.
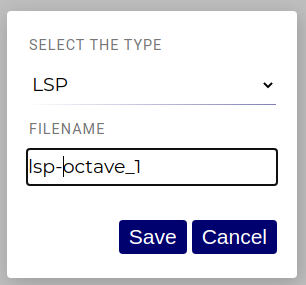
Navigate in WebMiau to the section where you want to create the LSP sheet. Right-click on the section, choose
"New Document", choose type "LSP" ("Language Sensitive Phrases").
Choose a name for the LSP sheet. In this example, we use "lsp-octave_1". Click "Save".
The LSP editor shows up. Define the LSP variables as in the screenshot below:
Publish it on the MUMIE server.
Connect lsp and problem (Not working in WebMiau -> contact us via Slack or Mail) and publish the problem to the
MUMIE Server too.
Open your problem on MUMIE Server:
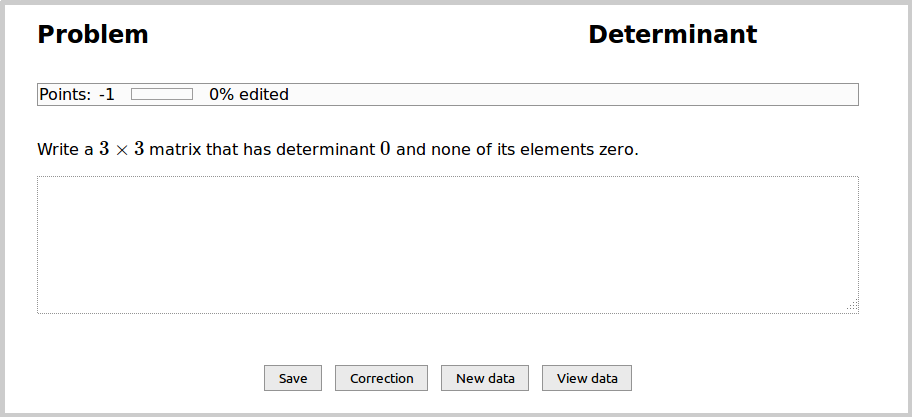
Play a bit around with the input field. First, fill in the sample solution, click "Save", and then "Correction".
The following shows up:
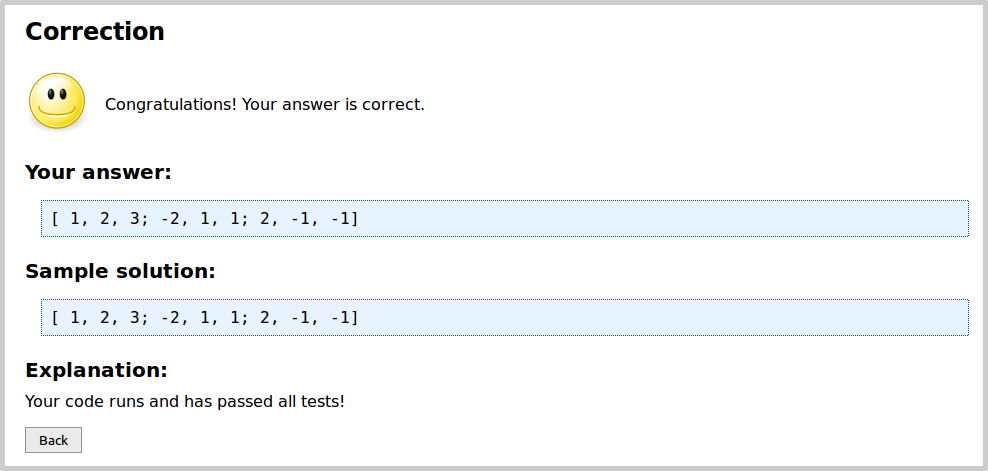
Next, fill in a wrong answer. For example, a matrix that is still $$3\times3$$ and has only non-zero elements,
but a determinant $$\neq 0$$. The correction is:
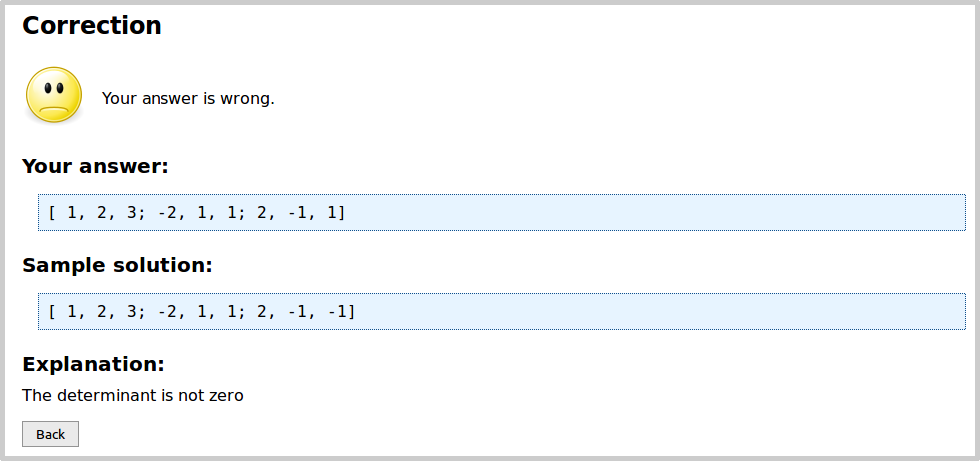
Try also matrices with wrong dimensions and matrices containing elements that are $$0$$.
What happens if the user answer isn't a matrix at all? In this case, Octave will fail to execute the evaluator, which is
recognized by the system automatically:
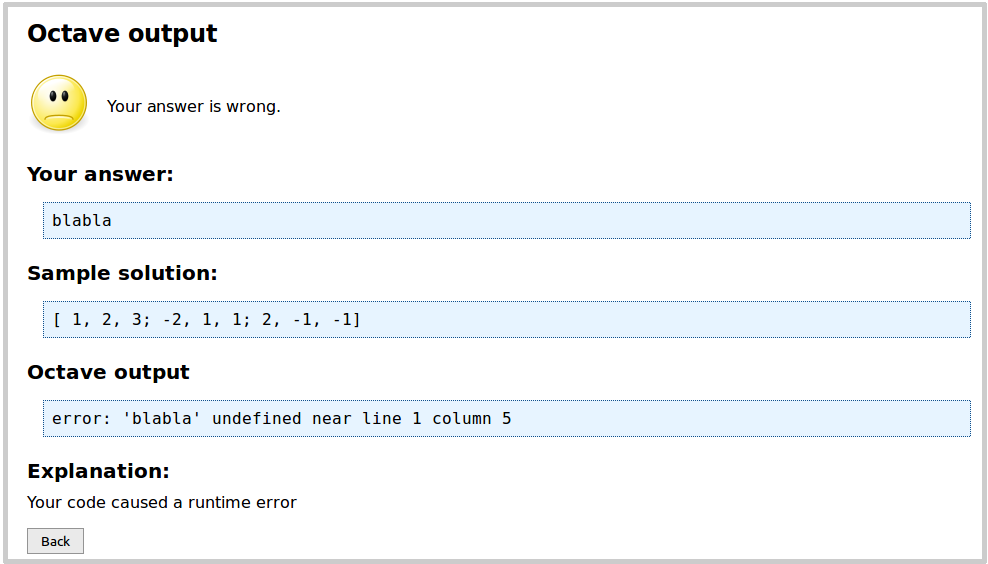
Recall that the author used the exit function in the evaluator to report the result of the check of the user answer.
What happens if the user, too, uses the exit function? If we try it, we get:
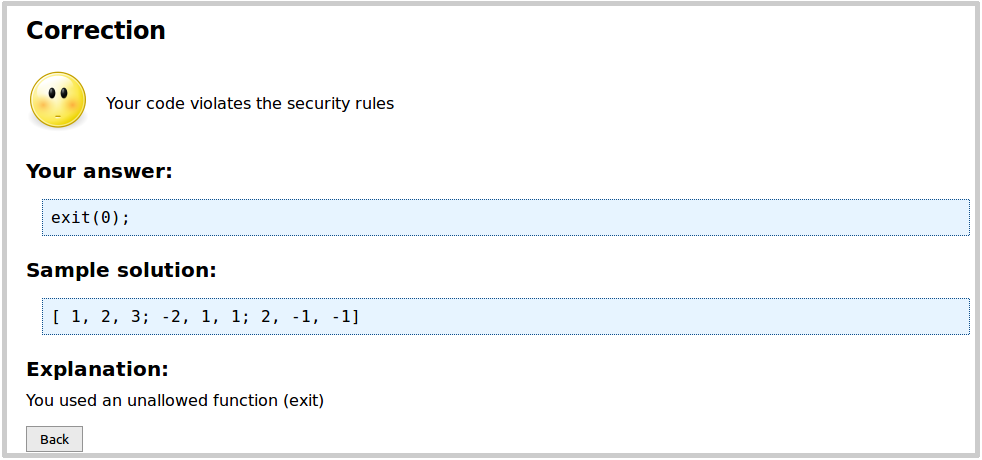
This is because all user input is checked for forbidden functions prior to execution. Clearly, exit is forbidden; so
are functions that read and write files and other I/O functions.
Example: More complex Octave problem
Here is an example of a more complex Octave problem. The user has to write a function that calculates the minimum of
all elements of a matrix.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 | \lang{en}{
\title{Minimum in a matrix}
Write a function called "matrix_min" that calculates the minimum of all elements
of a matrix. If the matrix is empty (thus, has no elements), the function should
return 0.
}
\octfunctionanswer{matrix_min}{12}{80}
\begin{hidden}
\begin{octfunctionsolution}{matrix_min}
function min = matrix_min (A)
min = 0;
started = 0;
for i = 1:rows(A)
for j = 1:columns(A)
a = A(i,j);
if ( or(started == 0, a < min) )
min = a;
endif
started = 1;
endfor
endfor
endfunction
\end{octfunctionsolution}
\begin{octfunction}{expected_matrix_min}
function min = expected_matrix_min (A)
min = 0;
started = 0;
for i = 1:rows(A)
for j = 1:columns(A)
a = A(i,j);
if ( or(started == 0, a < min) )
min = a;
endif
started = 1;
endfor
endfor
endfunction
\end{octfunction}
\begin{octfunction}{check_user_answer}
function check_user_answer (A, err_val)
expected = expected_matrix_min(A);
actual = matrix_min(A);
if ( actual != expected )
exit(err_val);
endif
endfunction
\end{octfunction}
\begin{octevaluator}
a_min = -10;
a_max = 10;
for i = 1:10
fac = a_min + rand(1) * (a_max - a_min);
A = fac * rand(2,2);
check_user_answer(A, 10);
endfor
A = zeros(0, 0);
check_user_answer(A, 11)
exit(0);
\end{octevaluator}
\octgrading{0}{1.0}{runs-and-passed-all-tests}
\octgrading{1}{0.0}{code-caused-runtime-error}
\octgrading{11}{0.5}{wrong-for-empty-matrices}
\end{hidden}
|