Mumie Wiki

You're not logged in

News

Index

Working with MUMIE as author

Working with MUMIE as teacher

Using MUMIE via plugin in local LMS

FAQ

Overview

Go back to the old wiki

We revise and update this wiki. We apologize for the inconvenience this may cause you.

Visualization Variables

Define variables

At the beginning of the genericGWTVisualization you can define variables. A variable can later be used to:

  1. create another variable that depends on this variable
  2. be displayed in the canvas (does not apply for number variables)
  3. be displayed in text-part as a formula, or number
1
2
\begin{variables}
\end{variables}

Random numbers

Supported are random integers, doubles, and rationals.

(!) Unlike the generic problem, the random variables only exists on runtime. It will be generated every time the page is reloaded. (!)

  1. randint

    1
    2
    \randint{name}{min}{max} %creates a random integer from [min, max] and store it as name
    \randint[Z]{name}{min}{max} %same as above, but avoiding zero

  2. randdouble

    1
    \randdouble{name}{min}{max} %creates a random real number between [min, max]

  3. randrat

    1
    \randrat{name}{minNumerator}{maxNumerator}{minDenominator}{maxDenominator} %creates a random rational number with numerator from [minNumerator, maxNumerator] and denominator from [minDenominator,maxDenominator]
Only numbers are allowed to be used as min and max value.

\randadjustIf

You can use \randadjustIf also in the variables environment of a generic visualization.

The syntax is the same as \randadjustIf in generic problems, but only random variables can be used in
the variables argument.

1
\randadjustIf{variables}{condition}

Example:

1
2
3
\randint[Z]{x1}{-5}{5}
\randint[Z]{x2}{-5}{5}
\randadjustIf{x1, x2}{x1 >= x2} % regenerate both x1 and x2 if x2 is not greater than x1.

Other variables

This group consists of numbers, functions and geometry variables. This type of variables can also be editable by the user and be dependant on other variables.
The common syntax of the variables is:

1
\type[editable]{name}{field}{value}

i

  • editable is an optional argument that enables user interactivity. If you use an editable variable later in
    a \text{}, then the user can edit it. If you put editable points, lines and vectors on a \plot{}, users are able to drag and move them around.
  • name is the name of the variable
  • field defines the number class. You can choose from integer, real, rational, complex, and operation
  • value defines the value of the variable. Here expressions are expected. Depending on the type it may
    have one or more comma separated expressions. You can use other variables by using the syntax var(name)

Examples

1. Numbers

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
%simply a number
\number{simple}{real}{0.5} % creates a real number with the value of 0.5
\number{sipmle2}{real}{1/2} % also creates 0.5
\number{simpleint}{integer}{0.5} % creates an integer with value 0
%complex
\number{c1}{complex}{1,-1} % creates a complex number with the value 1 - i
%operation
\number{op}{operation}{sin(pi)} % creates an operation sin(\pi)
%using other variables
\randint{randomA}{-5}{5} %create random value for a
\randint{randomB}{-5}{5} %create random value for b
\number[editable]{a}{integer}{var(randomA)} %creates an editable variable a with a random default value
\number[editable]{b}{integer}{var(randomB)} %creates an editable variable b with a random default value
\number{a+b}{operation}{var(a) + var(b)} %creates an operation a + b, where a and b will be replaced by the current value of a and b.
\number{result}{integer}{var(a)+var(b)} %creates an integer with the value of a+b. The value of result will be updated everytime the user edits either a or b.

Add a slider to manipulate your number variable

Numbers which are added to a graph can also be adjusted by a slider. To achieve this, define your number
as is done above and then use the following command inside the variables environment:

1
\slider[<step_size>]{<var_name>}{<num_var>}{<left_bound>, editable}{<right_bound>, editable}
  • var_name the variable name of the slider.
  • num_var the number that the slider will influence, an existing number variable must be used here and can be
    of type integer or real. If the variable number is editable, it will remain directly editable by the user. If the variable number is not editable, the number is only editable via the slider.
  • left_bound : the left bound value of the slider. Provide the extra parameter editable in order to make the bound editable by the user. The value should be a number and not a variable name.
  • right_bound : similar to left_bound but then regarding the right_bound value for the slider.

Optional parameters (displayed in square brackets)

  • step_size the step size with which the slider will adjust the number. The default value for numbers of type real
    is based on 100 steps between left and right bound, so a range of [0 10] would give a step size of 0.1. The default for numbers of type integer is _1_.
It is up to the author to make sure that step sizes and boundary values match up. When this is not the case, e.g. taking a left boundary of -1, right boundary of 9, a step size of two and initial number variable of 4; the slider might behave differently as expected.

The slider must then be added to the graph. The syntax for this is as following:

1
2
3
\begin{canvas}
  \slider{<slider_var1>, <slider_var2, ...}
\end{canvas}
  • Inside the canvas environment the \slider command is used to display the sliders defined in the variable environment.
  • Sliders can only be displayed in a canvas environment and not be used in a normal text environment.

A simple example of the syntax

1
2
3
4
5
6
\begin{variables}
  \number{n}{real}{-1}
  \slider[0.2]{n_slider}{n}{-5}{5, editable}
\end{variables}
 
\label{h}{$\textcolor{BLACK}{b =}$}

Results in the following: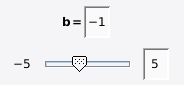
slider_example
with step sizes of 0.2.

Note that a slider can only be displayed in combination with a graph, see example below.

A complete example with a graph containing sliders

This example creates a graph which plots two points, (1) real number n and (2) absolute of number n.
Two sliders are created, both adjusting number n.

  • Slider 1 fixed range from -5 to 5 and default step size.
  • Slider 2 editable left (default -10) and right bound (default 10), with a step size of 1.

The points and the slider are then added to the canvas.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
\title{Absolutbetrag reeller Zahlen}
 
\text{Wählen Sie reelle Zahlen $a$ zwischen $-5$ und $5$ und
      beoachten Sie auf dem Zahlenstrahl die Zahl selbst und ihren Betrag $|a|$.}
 
\begin{variables}
  \number[editable]{n}{real}{-1}
  \slider{n_s1}{n}{-5}{5}
  \slider[1]{n_s2}{n}{-10, editable}{10, editable}
  \number{absn}{real}{absn(var(n))}
  \point{p1}{real}{var(n),0}
  \point{p2}{real}{var(absn),0}
\end{variables}
 
\label{n}{$n_1 =$}
 
\begin{canvas}
  \plotSize{500,80}
  \plotLeft{-6}
  \plotRight{6}
  \plot[numberLine]{p1,p2}
  \slider{n_s1, n_s2}
\end{canvas}

Results in the following: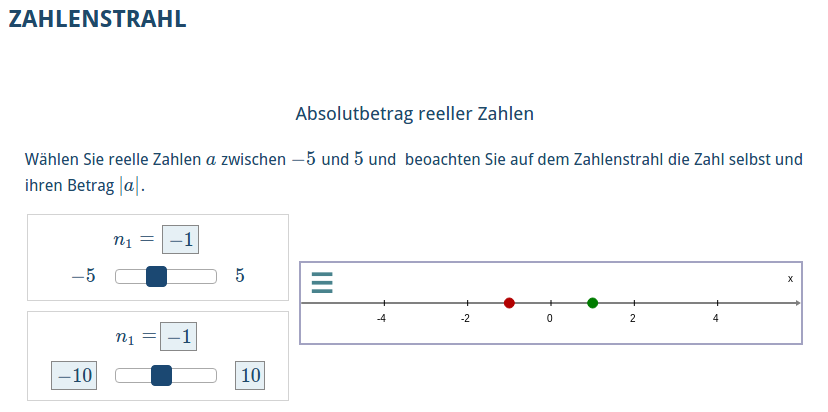
graph_with_slider.png

When adding a slider to the canvas the slider will be placed either to the left of the canvas (if there is enough room on the side), or at the top of the canvas (when there is not enough room). For this reason you might want to put content that is related to the slider number above the canvas.


In most cases you would probably want to add a label to the number variable (and not the slider variable) as it was done in both examples above. For more information on labels and their colors, see Adding color and label to variables

2. Function

1
\function{f}{real}{sin(x)}

3. Point

1
2
3
4
\point[editable]{p0}{real}{0,0} % creates an editable point at 0,0
\randint[Z]{a}{-3}{3}
\randint[Z]{b}{-3}{3}
\point[editable]{p1}{real}{var(a), var(b)} % creates an editable point with random default coordinate
You can extract the x and y coordinates of a point and use it as in *value* for other variables by using var(p1)[x] and var(p1)[y]

4. Line and Line Segment

Line and line segment expects you to use 2 point variables as value

1
2
\line{g}{real}{var(p0), var(p1)} % crates a line that runs through p0 and p1
\segment{g}{real}{var(p0), var(p1)} % crates a line segment between p0 and p1

5. Vector and Affine Vector

Vector is an arrow starting from the origin and ending at a point, the command expects only one point as value.
Affine vector expects as input two vectors. It is an arrow starting at the endpoint of the first vector, and being parallel to the second vector.

1
2
3
4
5
\point{p1}{real}{1,1}
\point{p2}{real}{3,0}
\vector{v1}{real}{var(p1)} % creates an arrow starting from origin to (1,1)
\vector{v2}{real}{var(p2)} % creates an arrow starting from origin to (3,0)
\affine{aff1}{real}{var(v1),var(v2)} % creates an arrow starting from (1,1) with coordinate (3,0)
Similar to points, you can extract the x and y coordinates of a vector and use it as in *value* for other variables by using var(v1)[x] and var(v1)[y]

6. Circle

1
2
\point{center}{real}{1,1}
\circle{c1}{real}{var(center), 2} %creates a circle on center with radius 2

7. Angle

1
2
\point{center}{real}{1,1}
\angle{c1}{real}{var(center), 2, 0, pi/2} %creates an angle on center with radius 2 from 0 to pi/2

8. Set

With set you can display section(s) of the 2d coordinate system (basically a set of (x,y)-tuple) that fulfills the given relation.

1
\set{set2}{real}{|var(p)x+var(q)y+var(c)|>var(d)}

Note that the value is a relation and you can combine relations with AND and OR. For example, to create a set equivalent to the above example, you can also use:

1
\set{set2}{real}{var(p)x+var(q)y+var(c)>var(d) OR -(var(p)x+var(q)y+var(c))>var(d)}

You can use the square brackets to group a part of the relation

1
\set{set2}{real}{y > 0 AND [x < -3 OR x > 3]}

9. Parametric Function in 2D

\parametricFunction plots a function with one parameter (t). The value of \parametricFunction has the following arguments:

  1. fx - the expression defining the x component
  2. fy - the expression defining the y component
  3. min - the lower bound of the parameter t
  4. max - the upper bound of the parameter t
  5. steps - number of vertices between the bounds
1
\parametricFunction{f}{real}{2abs(cos(2t))*cos(t)-3, 5*abs(sin(t))*sin(t)-3, 0, 2*pi, 1000}

10. Point on Curve

You can add a point to the graph of a function or to the curve of a parametric function by using the commands
\pointOnCurve or \pointOnParametricCurve.

\pointOnCurve has as the following arguments:

  1. (optional) limits for the function variable, default: -inf,inf
  2. name of the point
  3. number class
  4. function (explicit or the variable of a function)
  5. initial value of the function variable for the point
1
2
3
\function[editable]{f}{real}{sin(x)}
\pointOnCurve{p}{real}{var(f)}{1}
\pointOnCurve[0,2*pi]{q}{real}{cos(x)}{0}

\pointOnParametricCurve has as the following arguments:

  1. name of the point
  2. number class
  3. parametric function (explicit or the variable of a parametric function)
    (see above for details on the arguments of a parametric function)
  4. initial value of the function parameter t for the point
1
2
3
\parametricFunction{f}{real}{2abs(cos(2t))*cos(t), 5*abs(sin(t))*sin(t), 0, 2*pi, 1000}
\pointOnParametricCurve{p}{real}{var(f)}{0}
\pointOnParametricCurve{q}{real}{cos(t), sin(t), 0, 2*pi, 1000)}{pi}
The point in the canvas will be always editable, but non-editable in the text area above or below the canvas if added by \text{\$\var{<identifier of a point on curve>}\$}

3D Variables

This feature is currently not supported. We intend to enhance it again in the new framework that we are currently developing.

Updated by Andreas Maurischat, 4 years, 3 months ago – 297aca7