Normalize applies the following rules
Normalize and expand rules
This section will cover the rules that are applied when normalizing and/or expanding functions. But before we start on
that, take a look at the example below which explains shortly how functions are handled internally within MUMIE.
Example:
Take the following function: $$x^4 \cdot (3 + 2)$$. To enter this function into MUMIE, you would type the following:
x^4*(3+2), which in turn could be graphically displayed as the image below.
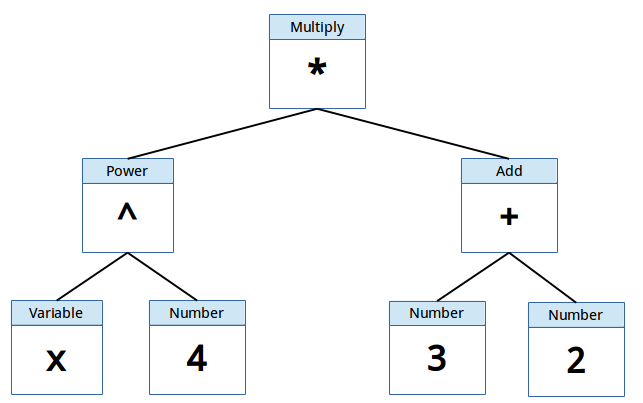
MUMIE uses the following terminology regarding the tree you see above.
- node referring to a box in the tree
- operation every node, together with its children, can be referred to as an operation.
The example above consists of the following operations
- Multiplication Operation (or simply MultiplicationOp)
- PowerOp,
- AddOp
- VariableOp and
- NumberOp.
Operations can be combined together to make more complex operations. The formula used above can therefor also be referred to as an operation.
Every node has the following properties:
and based on the type, possibly a:
- base (if it is a NumberOp)
- identifier (if it is a VariableOp)
Keeping this in our mind, we can take a look at the rules being applied when normalizing and/or expanding functions.
When normalizing/expanding, all rules will be applied until a stable state of the function has been reached, resulting in a normalized/expanded function. The rules for
normalization and expanding are shown below (showing the Class name of the Java-code in brackets), along with several examples for each rule.
Rules for normalizing functions
Collapse factors of a variable (NormalizeMultRule)
|
|
|
| $$3 \cdot 5 \cdot x$$ |
$$\Rightarrow$$ |
$$15x$$ |
| $$3 \cdot 5 \cdot x + 2 \cdot 4 \cdot y + 2 \cdot 3$$ |
$$\Rightarrow$$ |
$$15x+8y+2 \cdot 3$$ |
Collapse multiplications and additions (CollapseEqualOpsRule)
For addition:
|
|
|
| $$4+(3-4)$$ |
$$\Rightarrow$$ |
$$4+3-4$$ |
| $$3-(-4+x)$$ |
$$\Rightarrow$$ |
$$3+4-x$$ |
For multiplication:
|
|
|
| $$3 \cdot (4 \cdot 9 \cdot x)$$ |
$$\Rightarrow$$ |
$$3 \cdot 4 \cdot 9 \cdot x$$ |
| $$\frac{3}{\frac{1}{4} \cdot x}$$ |
$$\Rightarrow$$ |
$$\frac{3 \cdot 4}{x \cdot 1}$$ |
Collapse powers of i (CollapsePowerOfIRule)
|
|
|
| $$i^2$$ |
$$\Rightarrow$$ |
$$-1$$ |
| $$i^8$$ |
$$\Rightarrow$$ |
$$1$$ |
| $$i^{-7}$$ |
$$\Rightarrow$$ |
$$i$$ |
Evaluate expressions involving only numbers (PropagateConstantsRule)
|
|
|
| $$12.0+2.0^{3.0} \cdot 3$$ |
$$\Rightarrow$$ |
$$36$$ |
Evaluate expressions having zero as a factor (RemoveZeroMultRule)
|
|
|
| $$0 \cdot 3$$ |
$$\Rightarrow$$ |
$$0$$ |
| $$0 \cdot x$$ |
$$\Rightarrow$$ |
$$0$$ |
Evaluate powers with zero as exponent (RemoveZeroExponentRule)
|
|
|
| $$2x^{0}$$ |
$$\Rightarrow$$ |
$$2 \cdot 1$$ |
Collapse equal children belonging to addition operations (SummarizeEqualAddChildrenRule)
|
|
|
| $$y+2x + z - x$$ |
$$\Rightarrow$$ |
$$y+x+z$$ |
Collapse equal children belonging to multiplication operations (SummarizeEqualMultChildrenRule)
|
|
|
| $$x \cdot y \cdot x$$ |
$$\Rightarrow$$ |
$$x^2 \cdot y$$ |
| $$y \cdot x^2 \cdot z \cdot x^{-1}$$ |
$$\Rightarrow$$ |
$$y \cdot x \cdot z$$ |
Remove neutral elements (RemoveNeutralElementRule)
Only handles the following three cases
|
|
|
| $$x \cdot 1$$ |
$$\Rightarrow$$ |
$$x$$ |
| $$x \cdot -1$$ |
$$\Rightarrow$$ |
$$-x$$ |
| $$x + 0$$ |
$$\Rightarrow$$ |
$$x$$ |
Collapse powers (CollapsePowerRule)
Implements the following two rules:
|
|
|
| $$(a^b)^c$$ |
$$\Rightarrow$$ |
$$a^{bc}$$ |
| $$e^x$$ |
$$\Rightarrow$$ |
$$\exp(x)$$ |
Collapse powers when rational (CollapseRationalPowerRule)
If the node is a PowerOp with a rational exponent and the denominator of the exponent is n != 1 a n-th root node will be added as parent and the child will get the numerator as exponent.
|
|
|
| $$x^{\frac{3}{2}}$$ |
$$\Rightarrow$$ |
$$\sqrt{x^3}$$ |
Simplify constants of single nodes (NormalizeConstantRule)
Sets exponent to $$1$$ and factor to $$+/- 1$$ and calculates its base.
|
|
|
| $$(-2)^3$$ |
$$\Rightarrow$$ |
$$-8$$ |
Collapse function nodes that have their inverse function as child (CollapseInverseFunctionRule)
This rule only works on functions with a definded inverse function.
|
|
|
| $$\cos(\arccos(x))$$ |
$$\Rightarrow$$ |
$$x$$ |
| $$\ln(\exp(x))$$ |
$$\Rightarrow$$ |
$$x$$ |
Collapse function nodes for powers and n-roots (CollapseNrtRule)
This is a special case of the rule above.
|
|
|
| $$\sqrt{x^2}$$ |
$$\Rightarrow$$ |
$$\vert x \vert$$ |
Symmetry of elementary functions (HandleFunctionSymmetryRule)
Currently only applies to the following functions: @abs, acos, asin, atan, cos, cosh, n-root (for uneven n), sinh, sin and tan@. The rule is dependent on whether the function is symmetric or antisymmetric.
|
|
|
| $$\sin(-x)$$ |
$$\Rightarrow$$ |
$$-\sin(x)$$ |
| $$\vert -x \vert$$ |
$$\Rightarrow$$ |
$$\vert x \vert$$ |
Distributive law (NormalizeAddRule)
|
|
|
| $$3 \cdot (-x + 4)$$ |
$$\Rightarrow$$ |
$$-3x + 12$$ |
Rules for expanding functions
Distributive law (ExpandProductRule)
|
|
|
| $$4 \cdot (-b-3)$$ |
$$\Rightarrow$$ |
$$4 \cdot (-b) + 4 \cdot (-3)$$ |
Expand data in single node (ExpandInternalDataRule)
|
|
|
| $$-x^6$$ |
$$\Rightarrow$$ |
$$-1 \cdot x^6$$ |
Expands a power of products (ExpandPowerRule)
|
|
|
| $$(2 \cdot x)^4$$ |
$$\Rightarrow$$ |
$$2^4 \cdot x^4$$ |
Expands a power of sums (ExpandPowerOfSumRule)
|
|
|
| $$(2+x)^4$$ |
$$\Rightarrow$$ |
$$(2+x) \cdot (2+x) \cdot (2+x) \cdot (2+x)$$ |