Normalize applies the following rules

Normalize and expand rules
Rules for normalizing functions
Rules for expanding functions

Normalize and expand rules

This section will cover the rules that are applied when normalizing and/or expanding functions. But before we start on
that, take a look at the example below which explains shortly how functions are handled internally within MUMIE.

Example:
Take the following function: $$x^4 \cdot (3 + 2)$$. To enter this function into MUMIE, you would type the following:
x^4*(3+2), which in turn could be graphically displayed as the image below.

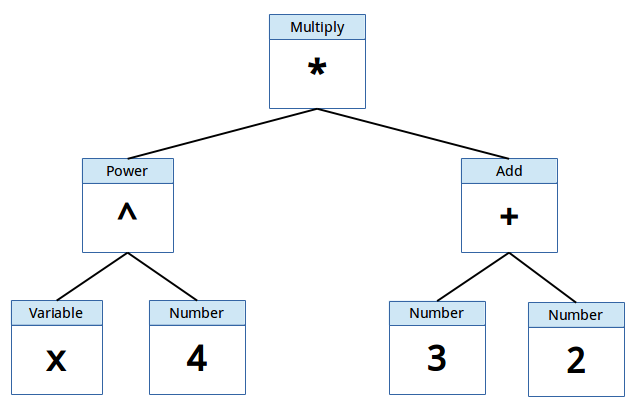
operation_tree

MUMIE uses the following terminology regarding the tree you see above.

node referring to a box in the tree
operation every node, together with its children, can be referred to as an operation.
The example above consists of the following operations
- Multiplication Operation (or simply MultiplicationOp)
- PowerOp,
- AddOp
- VariableOp and
- NumberOp.

Operations can be combined together to make more complex operations. The formula used above can therefor also be referred to as an operation.

Every node has the following properties:

factor
exponent

and based on the type, possibly a:

base (if it is a NumberOp)
identifier (if it is a VariableOp)

Keeping this in our mind, we can take a look at the rules being applied when normalizing and/or expanding functions.
When normalizing/expanding, all rules will be applied until a stable state of the function has been reached, resulting in a normalized/expanded function. The rules for
normalization and expanding are shown below (showing the Class name of the Java-code in brackets), along with several examples for each rule.

Rules for normalizing functions

Collapse factors of a variable (NormalizeMultRule)


$$3 \cdot 5 \cdot x$$	$$\Rightarrow$$	$$15x$$
$$3 \cdot 5 \cdot x + 2 \cdot 4 \cdot y + 2 \cdot 3$$	$$\Rightarrow$$	$$15x+8y+2 \cdot 3$$

Collapse multiplications and additions (CollapseEqualOpsRule)

For addition:


$$4+(3-4)$$	$$\Rightarrow$$	$$4+3-4$$
$$3-(-4+x)$$	$$\Rightarrow$$	$$3+4-x$$

For multiplication:


$$3 \cdot (4 \cdot 9 \cdot x)$$	$$\Rightarrow$$	$$3 \cdot 4 \cdot 9 \cdot x$$
$$\frac{3}{\frac{1}{4} \cdot x}$$	$$\Rightarrow$$	$$\frac{3 \cdot 4}{x \cdot 1}$$

Collapse powers of i (CollapsePowerOfIRule)


$$i^2$$	$$\Rightarrow$$	$$-1$$
$$i^8$$	$$\Rightarrow$$	$$1$$
$$i^{-7}$$	$$\Rightarrow$$	$$i$$

Evaluate expressions involving only numbers (PropagateConstantsRule)


$$12.0+2.0^{3.0} \cdot 3$$	$$\Rightarrow$$	$$36$$

Evaluate expressions having zero as a factor (RemoveZeroMultRule)


$$0 \cdot 3$$	$$\Rightarrow$$	$$0$$
$$0 \cdot x$$	$$\Rightarrow$$	$$0$$

Evaluate powers with zero as exponent (RemoveZeroExponentRule)


$$2x^{0}$$	$$\Rightarrow$$	$$2 \cdot 1$$

Collapse equal children belonging to addition operations (SummarizeEqualAddChildrenRule)


$$y+2x + z - x$$	$$\Rightarrow$$	$$y+x+z$$

Collapse equal children belonging to multiplication operations (SummarizeEqualMultChildrenRule)


$$x \cdot y \cdot x$$	$$\Rightarrow$$	$$x^2 \cdot y$$
$$y \cdot x^2 \cdot z \cdot x^{-1}$$	$$\Rightarrow$$	$$y \cdot x \cdot z$$

Remove neutral elements (RemoveNeutralElementRule)

Only handles the following three cases


$$x \cdot 1$$	$$\Rightarrow$$	$$x$$
$$x \cdot -1$$	$$\Rightarrow$$	$$-x$$
$$x + 0$$	$$\Rightarrow$$	$$x$$

Collapse powers (CollapsePowerRule)

Implements the following two rules:


$$(a^b)^c$$	$$\Rightarrow$$	$$a^{bc}$$
$$e^x$$	$$\Rightarrow$$	$$\exp(x)$$

Collapse powers when rational (CollapseRationalPowerRule)

If the node is a PowerOp with a rational exponent and the denominator of the exponent is n != 1 a n-th root node will be added as parent and the child will get the numerator as exponent.


$$x^{\frac{3}{2}}$$	$$\Rightarrow$$	$$\sqrt{x^3}$$

Simplify constants of single nodes (NormalizeConstantRule)

Sets exponent to $$1$$ and factor to $$+/- 1$$ and calculates its base.


$$(-2)^3$$	$$\Rightarrow$$	$$-8$$

Collapse function nodes that have their inverse function as child (CollapseInverseFunctionRule)

This rule only works on functions with a definded inverse function.


$$\cos(\arccos(x))$$	$$\Rightarrow$$	$$x$$
$$\ln(\exp(x))$$	$$\Rightarrow$$	$$x$$

Collapse function nodes for powers and n-roots (CollapseNrtRule)

This is a special case of the rule above.


$$\sqrt{x^2}$$	$$\Rightarrow$$	$$\vert x \vert$$

Symmetry of elementary functions (HandleFunctionSymmetryRule)

Currently only applies to the following functions: @abs, acos, asin, atan, cos, cosh, n-root (for uneven n), sinh, sin and tan@. The rule is dependent on whether the function is symmetric or antisymmetric.


$$\sin(-x)$$	$$\Rightarrow$$	$$-\sin(x)$$
$$\vert -x \vert$$	$$\Rightarrow$$	$$\vert x \vert$$

Distributive law (NormalizeAddRule)


$$3 \cdot (-x + 4)$$	$$\Rightarrow$$	$$-3x + 12$$

Rules for expanding functions

Distributive law (ExpandProductRule)


$$4 \cdot (-b-3)$$	$$\Rightarrow$$	$$4 \cdot (-b) + 4 \cdot (-3)$$

Expand data in single node (ExpandInternalDataRule)


$$-x^6$$	$$\Rightarrow$$	$$-1 \cdot x^6$$

Expands a power of products (ExpandPowerRule)


$$(2 \cdot x)^4$$	$$\Rightarrow$$	$$2^4 \cdot x^4$$

Expands a power of sums (ExpandPowerOfSumRule)


$$(2+x)^4$$	$$\Rightarrow$$	$$(2+x) \cdot (2+x) \cdot (2+x) \cdot (2+x)$$

News